Senar, Pipa Organa Terbuka - Tertutup ǀ Penjelasan, Penurunan Persamaan (Rumus), Analisis Gambar, & Contoh Penerapannya

Setelah belajar tentang gelombang bunyi, kita akan membahas terkait senar (string), pipa organa terbuka (open organ pipe), dan pipa organa tertutup (closed organ pipe). Berikut penjelasan, penurunan persamaan (rumus), analisis gambar, dan contoh penerapannya.

Baca sebelumnya : Efek Doppler ǀ Penjelasan, Penurunan Persamaan (Rumus), Analisis Gambar, & Contohnya

SENAR (STRING)

Perhatikan gambar 1.1., sebuah senar diikatkan pada masing-masing ujungnya. Tegang senar pada nada dasar berbeda dengan tegang senar pada nada atas pertama. Semakin tegang senar, maka akan semakin tinggi frekuensi-nya walau panjang ujung ke ujungnya sama.

Gambar 1.1. Frekuensi Senar Nada Dasar, Nada Atas Pertama, Nada Atas Kedua, . . dan Penurunannya
-klik gambar untuk melihat lebih baik-

Salah satu contoh penerapan pada senar tegang ini adalah senar gitar akustik, biola, kecapi, bass, dll. Kita mendapati senar yang dapat kita atur ketegangannya dengan memutar di bagian ujung gitar.

Saat masing-masing senar dipetik, gelombang muncul seperti pada gambar. Besar amplitudonya sama tetapi frekuensi-nya berbeda. Perbandingan frekuensi nada dasar, nada atas pertama, nada atas kedua, dan seterusnya

PERBANDINGAN FREKUENSI SENAR

f0 : f1 : f2 : . . . = 1/2 : 1 : 3/2 : . . . atau = 1 : 2 : 3 : . . .

Kita dapat melihat-nya dari f0 = v/2L ; f1 = v/L ; f2 = 3/2L. Masing-masing frekuensi memiliki bilangan 1/2, 1, dan 3/2.

Dari persamaan gambar 1.1., kita juga dapat merumuskan sebuah persamaan n untuk mencari λ_n dan f_n, karena kita tidak mungkin menggambar jika ditanyakan nada atas ke-10. Begitupula nilai frekuensi-nya.

PERSAMAAN N UNTUK λ_n DAN f_n PADA SENAR

λ_n = 2L/(n+1)

f_n = v/ λ_n = (n+1)v/2L

PIPA ORGANA TERBUKA (OPEN ORGAN PIPE)

Perhatikan gambar 1.2., sebuah pipa atau kolom udara yang tiap ujung-nya terbuka. Gelombang bunyi yang diberikan pada masing-masing nada berbeda frekuensinya. Hal ini menyebabkan banyaknya gelombang pada panjang pipa L atau kolom udara berbeda pada masing-masing nada.

Gambar 1.2. Frekuensi Pipa Organa Terbuka Nada Dasar, Nada Atas Pertama, Nada Atas Kedua, . . dan Penurunannya
-klik gambar untuk melihat lebih baik-

Salah satu contoh penerapan pipa organa terbuka adalah seruling, angklung, shakuhachi, botol kaca berisi air yang dipukul dibagian tengahnya, dll. Tetapi dalam penerapan ada yang sedikit berbeda.

Alat musik di atas memanfaatkan kolom udara yang panjangnya berbeda-neda untuk menghasilkan frekuensi yang diinginkan. Sedangkan, pembahasan kita kolom udaranya sama tetapi frekuensinya dibuat berbeda.

Perbandingan frekuensi, panjang λ, persamaan λ_n, f_n, pada pipa organa terbuka sama dengan senar. Mereka hanya dibedakan pada bentuk gelombangnya saja.

PERBANDINGAN FREKUENSI PIPA ORGANA TERBUKA

f0 : f1 : f2 : . . . = 1/2 : 1 : 3/2 : . . . atau = 1 : 2 : 3 : . . .

Kita dapat melihat-nya dari f0 = v/2L ; f1 = v/L ; f2 = 3/2L. Masing-masing frekuensi memiliki bilangan 1/2, 1, dan 3/2.

Dari persamaan gambar 1.2., kita juga dapat merumuskan sebuah persamaan n untuk mencari λ_n dan f_n. Begitupula nilai frekuensi-nya.

PERSAMAAN N UNTUK λ_n DAN f_n PADA PIPA ORGANA TERBUKA

λ_n = 2L/(n+1)

f_n = v/ λ_n = (n+1)v/2L

PIPA ORGANA TERTUTUP (CLOSED ORGAN PIPE)

Perhatikan gambar 1.3., sebuah pipa atau kolom udara yang salah satu ujung-nya terbuka dan yang lainnya tertutup. Gelombang bunyi yang diberikan pada masing-masing nada berbeda frekuensinya. Hal ini menyebabkan banyaknya gelombang pada panjang pipa L atau kolom udara berbeda pada masing-masing nada.

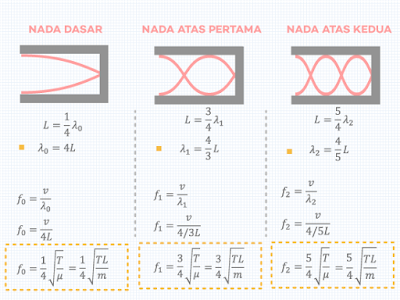Gambar 1.3. Frekuensi Pipa Organa Tertutup Nada Dasar, Nada Atas Pertama, Nada Atas Kedua, . . dan Penurunannya
-klik gambar untuk melihat lebih baik-

Salah satu contoh penerapan pipa organa tertutup adalah klarinet, terompet, pan-pipes, botol kaca berisi air yang ditiup mulut botol-nya, atau gelas wine yang digesek pada bagian bibi gelas-nya, dll.

PERBANDINGAN FREKUENSI PIPA ORGANA TERBUKA

f0 : f1 : f2 : . . . = 1/4 : 3/4 : 5/4 : . . . atau = 1 : 3 : 5 : . . .

Kita dapat melihat-nya dari f0 = v/4L ; f1 = 3v/4L ; f2 = 5/4L. Masing-masing frekuensi memiliki bilangan 1/4, 3/4, dan 5/4.

Dari persamaan gambar 1.3., kita juga dapat merumuskan sebuah persamaan n untuk mencari λ_n dan f_n. Begitupula nilai frekuensi-nya.

PERSAMAAN N UNTUK λ_n DAN f_n PADA PIPA ORGANA TERTUTUP

λ_n = 4L/(2n+1)

f_n = v/ λ_n = (2n+1)v/4L

Baca selanjutnya : -

Itulah penjelasan, penurunan persamaan (rumus), analisis gambar, dan contoh penerapan dari senar (string), pipa organa terbuka (open pipes), dan pipa organa tertutup (closed pipes).