Osilasi (Getaran) ǀ Penurunan Persamaan Gelombang Sinusoidal, Merubah Getaran menjadi Grafik Sinus & Lingkaran
Pembahasan kali ini, kita akan membahas
tentang getaran (osilasi), pengertian, penurunan persamaannya, hubungannya
terhadap grafik gelombang sinusoidal, dan cara merubah gerak getaran menjadi
grafik gelombang atau lingkaran untuk mengetahui sudutnya.
GETARAN (OSCILLATION)
Osilasi (vibrasi atau
getaran atau gerak periodik) adalah gerak bolak-balik terhadap titik setimbang.
Jika waktu selama gerak bolak-balik ini konstan, maka osilasi tersebut adalah
gerak harmonis.
Salah satu contoh yang dapat kita
pelajari adalah gerak bandul dan gerak pegas pada gambar 1.1. Titik
setimbang pada bandul dan pegas berada saat x=0. Saat bandul atau pegas
disimpangkan, akan muncul gaya pemulih yang mengarah ke titik setimbang begitu
seterusnya.
 |
| Gambar 1.1. Osilasi (Getaran) pada Bandul dan Pegas -klik gambar untuk melihat lebih baik- |
NB : Kita akan mempelajari gaya
pemulih dan getaran lebih lanjut pada pembahasan berikutnya. Kali ini, kita
akan fokus pada runtutan persamaan (rumus) dan korelasi antara getaran,
gelombang, dan sudut pada gelombang.
Satu getaran penuh berarti dari
titik 1,2,3,4,5. Waktu yang dibutuhkan untuk menyelesaikan satu getaran penuh adalah
T (periode). Kita dapat memilih posisi awal (nol) getaran. Mulai dari tengah
atau saat bandul disimpangkan. Getaran ini diam ditempat dan tidak mengganggu
medium sekitar.
GELOMBANG (GETARAN YANG MERAMBAT)
Misal, pegas pada gambar 1.1.c
digantung vertikal dan mengganggu air yang tenang. Getaran (osilasi) ini akan
merambat pada medium air dan meluas. Getaran yang merambat inilah yang
disebut dengan gelombang.
GELOMBANG SINUSOIDAL
Pada pembahasan ini, kita akan sering menyinggung gelombang sinusoidal. Kata ini dapat bermakna benar-benar “gelombang” atau “grafik” yang menyerupai gelombang. Kata “sinusoidal” bermakna ia mirip dengan grafik sinus, yaitu mulai dari titik 1,2,3,4,5 (bukit-lembah) pada gambar 1.2.b. Jadi, harap dipahami.
 |
| Gambar 1.2. Merubah Gerak Getaran menjadi Grafik Gelombang Sinusoidal dan Lingkaran, dimana Titik P adalah Titik Sembarang -klik gambar untuk melihat lebih baik- |
Kita dapat membuat sebuah grafik gelombang
sinusoidal dan lingkaran dari getaran bandul ataupun pegas, seperti pada gambar
1.2. Saat bandul bergerak dari titik 1 ke 2, sama dengan ¼ gelombang
dari titik 1 ke 2 grafik gelombang sinusoidal, dan nilai sudutnya terhadap adalah
90 derajat dilihat dari grafik lingkaran.
Sampai akhir pembahasan kita akan sepakat membuat grafik gelombang dimulai dari titik 0, lalu disimpangkan ke +x, dan kembali ke titik 0 persis seperti gambar 1.2. gelombang sinusoidal. Apakah boleh memulainya dari titik +x? Boleh, kita lakukan ini agar tidak membingungkan.
PERBEDAAN PERSAMAAN GETARAN YANG BEDA KONDISI AWAL
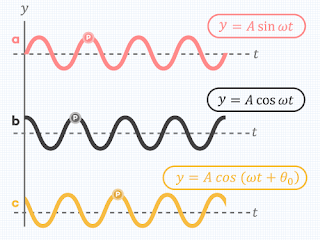
Persamaan (rumus) ini dapat kita gunakan pada getaran (osilasi) dan gelombang. Kita hanya memerlukan beberapa penyesuaian, jadi harap dipahami. Perhatikan gambar 1.3., persamaan (rumus) posisi = y titik P yang diletakkan sembarang pada gelombang a,b, dan c ternyata berbeda.
Gambar 1.3. Grafik Posisi-Waktu yang Berbentuk Gelombang Sinusoidal dengan Kondisi Awal Gelombang yang Berbeda-beda.
Pada dasarnya, ketiga kondisi ini dapat menggunakan persamaan sin (semua)
-klik gambar untuk melihat lebih baik-
Hal ini terjadi karena awalan pada
gelombang sinusoidal berbeda. Kita akan menggunakan persamaan sin dengan acuan gelombang
a saja (bukit-lembah). Mengapa muncul simbol tetha dan titik P diletakkan
sembarang?
Tetha adalah perbedaan kondisi awal
dari gelombang yang perlu kita tambahka. Kita anggap gelombang a berada kondisi awal nol,
maka tetha-nya adalah nol dan kita tidak perlu ditulis. Sekarang, kita boleh anggap
gelombang b juga berada pada kondisi awal nol, maka tetha-nya adalah nol dengan
syarat mengganti sin menjadi cos.
Jika kita memaksa menggunakan
persamaan sin pada gambar 1.3.b, maka kita perlu menambahkan tetha.
Dan gelombang c, kita memilih
rujukan persamaan cos pada gelombang b. Kita anggap kondisi nol itu seperti
gelombang b. Berarti gelombang c adalah gelombang b dengan menambahkan tetha agar sama dengan gelombang b.
Titik P sebagai titik yang dicari
diletakkan sembarang karena posisi nya tinggal bergantung pada nilai t (waktu)
yang kita masukkan. Jadi, titik P contoh di atas dibuat random saja
tanpa ada maksud lain.
PENURUNAN PERSAMAAN GETARAN
Sekarang, kita gunakan acuan kondisi nol dari getaran adalah seperti pada gambar 1.3. a. Kita gunakan persamaan sin. Berikut penurunan persamaan (rumus) posisi simpangan titik P gelombang sinusoidal, kecepatan, dan percepatannya. y atau x = A sin omega.t ; v = -omega.A cos (omega.t) ; a = -omega kuadrat. A sin (omega.t).
 |
| Gambar 1.4.a. Penurunan Persamaan Posisi Gelombang Sinusoidal -klik gambar untuk melihat lebih baik- |
 |
| Gambar 1.4.b. Penurunan Persamaan Posisi Gelombang Sinusoidal, Frekuensi Sudut (Kecepatan Sudut), Periode, dan Frekuensi Gelombang -klik gambar untuk melihat lebih baik- |
Kita akan menjabarkan nilai psi pada persamaan 8,9, dan 10 atau yang sering muncul. Psi akan ditambahkan saat gelombang tidak dimulai dari titik setimbang x=0 atau kita mencari posisi, kecepatan, percepatan suatu titik dengan acuan titik tertentu yang random.
APA ITU PSI PADA PERSAMAAN GELOMBANG SINUSOIDAL?
Bukankah tadi persamaan sin ini
digunakan saat grafik gelombang berbentuk (bukit-lembah) seperti pada gambar
1.3.a.? Tetha tidak akan muncul saat kondisi awal ini sesuai, sin dan kondisi awal x=0. Jika ia turun lalu
naik atau dimulai dari tengah bukit gelombang, maka kita dapat tambahkan tetha.
Sebagai alternatif untuk kondisi
gelombang 1.3 b yang dimulai dari perut gelombang, kita dapat menggunakan cos
tanpa tambahan tetha. Sebenarnya, kita dapat menggunakan sin tetapi harus
ditambah tetha. Perhatikan gambar berikut.
 |
| Gambar 1.5. Perbedaan Persamaan Sin dan Cos pada Gelombang Sinusoidal. Pada gambar a, kita menerapkan persamaan sin. Pada gambar b, kita dapat menerapkan persamaan cos atau sin yang ditambah tetha. Tetha adalah kondisi awal dari grafik gelombang yang harus ditambahkan. |
PERSAMAAN LAIN DARI SIMPANGAN
Berikut penurunan persamaan simpangan y atau x = A
sin (omega.t + kx) dari persamaan gelombang sinusoidal.
 |
| Gambar 1.6. Asal Persamaan Gelombang Sinusoidal dengan y atau x = A sin (omega.t+kx) -klik gambar untuk melihat lebih baik- |
KESIMPULAN
Osilasi adalah getaran. Getaran yang merambat disebut dengan gelombang. Gelombang sinusoidal dapat berarti “gelombang” atau “grafik” yang menyerupai gelombang. Kita dapat merepesentasikan gerak getaran menjadi grafik gelombang sinusoidal dan lingakaran. Penurunan persamaan posisi simpangan dari sebuah titik dapat menggunakan persamaan sin atau cos dan tetha karena perbedaan posisi awal.