Osilasi (Getaran) Bandul Sederhana ǀ Penjelasan & Penurunan Persamaan (Rumus)

Osilasi (getaran) pendulum atau bandul adalah gerak bolak-balik pendulum terhadap titik setimbangnya. Jika waktu selama bolak-balik itu bernilai konstan, maka osilasi tersebut termasuk gerak harmonis. Berikut penjelasan, penurunan persamaan (rumus) gerak harmonis sederhana bandul.

Baca sebelumnya : Osilasi (Getaran) ǀ Penurunan Persamaan Gelombang Sinusoidal, Merubah Getaran menjadi Grafik Sinus & Lingkaran

BANDUL (PENDULUM) SEDERHANA

Bandul sederhana dapat dikatakan bergerak harmonis jika simpangan bandul terhadap sumbu y adalah kurang dari 10 derajat (>10^o). Jika lebih dari itu, maka kita tidak dapat menyebut bandul bergerak secara harmonis. Hal ini terjadi karena sudut simpangan yang besar akan menyebabkan simpangan tidak konstan (teredam).

Pada dasarnya, kita anggap bandul bergerak tanpa gesekan dari medium sekitar (udara) atau ia bergerak selamanya tanpa berhenti. Dalam kehidupan nyata, hal ini tentu tidak mungkin. Kita dapat menemukan perhitungan yang sesuai saat sudut kita perkecil (kurang dari 10 derajat).

SATU GETARAN PENUH GERAK BANDUL

Perhatikan gambar 1.1., satu getaran penuh bandul adalah saat bandul bregerak dari suatu posisi melewati titik setimbang dan kembali ke posisinya semula. Titik setimbang pada bandul adalah titik B.

Jika bandul berangkat dari titik A, maka satu getaran penuh adalah A-B-C-B-A. Jika kita menghitung dari titik B, maka satu getaran penuh adalah B-C-B-A-B. Pada saat bandul disimpangkan sebesar θ, gaya pemulih muncul pada bandul. Arah gaya pemulih ini selalu menuju titik setimbang (titik B).

BESARAN PADA GERAK BANDUL

Besar gaya pemulih F pada bandul adalah mg.sinθdengan arah menuju B. Saat bandul di titik A, gaya pemulih menuju titik B. Saat bandul di titik C, gaya pemulih menuju titik B juga.

Pada gambar 1.1., bandul digantung pada sebuah tali sepanjang l. Gaya tegang tali T muncul sepanjang tali. Bandul yang memiliki massa m menyebabkan bandul memiliki gaya berat mg. Kita dapat menguraikan gaya-gaya ini terhadap sumbu x dan y.

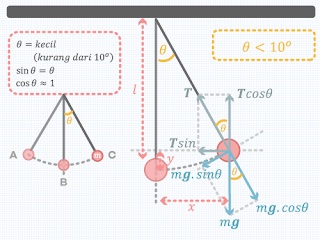Gambar 1.1. Komponen Gaya pada Gerak Bandul (Pendulum) Sederhana terhadap Sumbu x dan y
-klik gambar untuk melihat lebih baik-

Ingat! gaya tegang tali T = mg bukan mg.cosθ. Kita dapat mengidentifikasinya melalui penurunan persamaan, gambar gaya, atau saat tali berada pada titik setimbang (titik B)

Sudut θ yang kurang dari sepuluh derajat menyebabkan nilai sin θ-nya sama dengan nilai θ-nya, nilai cos θ-nya mendekati 1. Penurunan persamaan (rumus) dari gerak bandul dapat dilihat pada gambar 1.2.

Simpangan bandul ditandai sebagai besaran x dan y. Simpangan x maksimal pada bandul dinamakan amplitudo. Perhatikan gambar 1.1 yang bertuliskan x dan y.

PENURUNAN PERSAMAAN (RUMUS) BANDUL

Gambar 1.2. Penurunan Persamaan pada Gerak Bandul (Pendulum) Sederhana pada Gerak Harmonis Sederhana
-klik gambar untuk melihat lebih baik-

Dalam menemukan persamaan-persamaan yang berlaku pada gerak bandul sederhana ini, kita dapat subtitusi antara gaya total yang bekerja pada bandul terhadap sumbu x dan sumbu y.

Ingat! Besaran x double dot dan y double dot adalah penulisan dalam bentuk lain dari a (percepatan). Percepatan x berarti percepatan sepanjang sumbu x dan percepatan y adalah percepatan sepanjang sumbu y. Harap dipahami dan tidak bingung.

Perpindahan x pada bandul adalah ke kanan atau ke kiri. Perpindahan y pada bandul berarti ke atas atau ke bawah. Pada gerak bandul sederhana, perpindahan terhadap sumbu y ini kecil sekali sehingga percepatan terhadap sumbu y-nya juga akan semakin kecil (y kecil, maka ÿ = a_y akan makin kecil).

Baca selanjutnya : Osilasi (Getaran) Pegas Horisontal & Vertikal ǀ Penjelasan & Penurunan Persamaan (Rumus)

KESIMPULAN

Gerak bandul sederhana akan dikatakan harmonis jika sudut simpangannya kurang dari 10 derajat. Penurunan persamaan (rumus) pada bandul menunjukkan bahwa x maksimal dinamakan amplitudo, T=mg, ω = akar (g/l).