Momentum Sudut Benda (Partikel Bermassa) ǀ Pengertian, Penurunan Persamaan, & Contoh pada Kehidupan

Pada gerak translasi, kita membahas tentang momentum linier (linear momentum) sebuah partikel bermassa dan benda kaku bermassa. Bagaimana dengan partikel dan benda kaku pada gerak melingkar? Kita akan mengenal momentum sudut. Berikut pengertian, penurunan persamaan, dan contoh momentum sudut.

Seorang atlet sepatu roda meluncur di atas lantai dengan kecepatan tertentu. Seketika ia mendekati tiang, ia memegangnya dan hal itu membuatnya bergerak memutar – mutar. Saat atlet meluncur lurus, ia memiliki momentum linier. Begitupula, saat ia bergerak memutar. Kita tidak akan mendapati momentum linier melainkan momentum sudut.

Baca sebelumnya : Gerak Menggelinding di Bidang Datar & Miring ǀ Pengertian, Penurunan Persamaan, & Perbedaannya dengan Gerak Translasi atau Rotasi

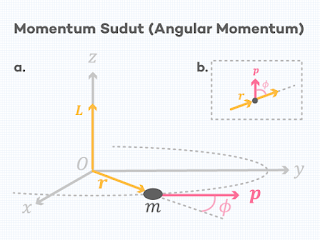
MOMENTUM SUDUT (ANGULAR MOMENTUM)

Momentum sudut (angular momentum) adalah sebuah besaran vektor hasil perkalian silang vektor posisi (r) dan momentum linier (p), dimana p adalah massa (m) kali kecepatan (v). Semakin besar massa akan semakin besar momentum sudutnya dan semakin besar kecepatan tangensial atau liniernya (v) semakin besar pula momentum sudutnya.

Kita dapat bayangkan sebuah roda gigi besi besar berputar dengan cepat dan berputar dengan pelan. Tentu, roda gigi besar yang bergerak cepat lebih berbahaya dibanding yang pelan. Tidak hanya itu, walaupun roda gigi besi tersebut kecil tetapi berputar cepat, ia juga sama bahayanya.

Perhatikan gambar 1.1.a, sebuah patikel bermassa m diberi kecepatan (v) dengan arah yang sama dengan momentum liniernya (p). Jarak posisi partikel terhadap poros putar adalah (r). Sebuah sudut terbentuk antara vektor posisi (r) dan momentum linier (p). Partikel tersebut bergerak pada sebuah lintasan melingkar.

Partikel Bermassa yang Bergerak Melingkar. Kecepatan tangensial (v) searah dengan momentum linier (p) karena p=mv, sedangkan arah momen gaya (torsi) searah dengan momentum sudut (L).

Gambar 1.1. Partikel Bermassa yang Bergerak Melingkar
Kecepatan tangensial (v) searah dengan momentum linier (p) karena p=mv, sedangkan arah momen gaya (torsi) searah dengan momentum sudut (L).
- klik gambar untuk melihat lebih baik -

ARAH VEKTOR MOMENTUM SUDUT (L) SEJAJAR DENGAN ARAH MOMEN GAYA (TORSI)

Arah momentum sudut (L) berada tegak lurus terhadap (p) dan (r), dimana arah momentum sudut (L) ini juga sama dengana arah momen gaya (torsi). Cara menentukan arah vektor ini dapat dilakukan dengan kaidah tangan kanan. Empat jari tangan untuk arah (r), lalu disapukan ke arah (p), dimana ibu jari akan mengarah ke arah (L).

PENURUNAN PERSAMAAN MOMENTUM SUDUT (L)

Perhatikan gambar 1.1. b, jika momentum linier (p) membentuk sudut terhadap vektor posisi (r), maka (p) yang digunakan adalah yang tegak lurus terhadap (r), dimana nilainya adalah sinφ. Jika sudut yang dibentuk 90 derajat, maka nilainya satu dan nol untuk sudut 0 atau 180 derajat.

Gambar 1.2. Penurunan Persamaan Momentum Sudut dan Hubungannya dengan Momentum Linier

- klik gambar untuk melihat lebih baik -

Dari pernyataan di atas dapat disimpulkan bahwa partikel tidak akan berputar jika kecepatan (v) (dimana p = mv) sejajar dengan vektor posisi (r) atau menuju arah radial terhadap poros putar (ke luar atau dalam).

Pada persamaan (7) gambar 1.2, kita dapat melihat kesamaan antara gaya rotasi dan gaya translasi, dimana gaya translasi adalah F dan gaya untuk rotasi adalah (torsi). Momentum linier digunakan untuk gerak translasi dan momentum sudut digunakan untuk gerak rotasi.

Ingat! Persamaan (4) hanya berlaku untuk momentum sudut yang memiliki arah vektor yang satu tangkap dengan momen gayanya (torsi).

APAKAH MOMENTUM SUDUT KHUSUS UNTUK GERAK ROTASI?

Tentu, tidak. Semua gerak dapat dikaitkan dengan momentum sudut asalkan ia memiliki sumbu yang memiliki jarak terhadap sampel massa yang ditanyakan.

Sebagai contoh sebuah mobil tengah melintas di bawah menara eifel. Kita akan menentukan puncak menara eifel sebagai sumbu yang dimaksud. Momentum linier (p) bergerak searah jalan atau lintasan lurus. Kita akan menemukan vektor posisi (r) antara massa mobil dan puncak menara.

Baca selanjutnya : Momentum Sudut Benda (Kaku) ǀ Hubungan dengan Momen Inersia, Penurunan Persamaan, & Hukum Kekekalan Momentum Sudut

KESIMPULAN

Contoh momentum sudut itu tidak melulu soal gerak melingkar karena hal ini tergantung acuan yang kita gunakan, acuan diam seperti puncak menara eifel. Momentum sudut diperoleh dengan mengalikan momentum linier dan jari-jari dari penurunan persamaan hukum newton 2 alternatif.