Momentum Sudut Benda (Kaku) ǀ Hubungan dengan Momen Inersia, Penurunan Persamaan, & Hukum Kekekalan Momentum Sudut

Bagaimana jika yang diputar adalah sebuah benda kaku dengan berbagai variasi bentuk dan poros? Kita dapat menurunkan persamaan momentum sudut (L) benda kaku dari persamaan sebelumnya dan hubungannya dengan momen inersia (I). Berikut momentum sudut benda kaku yang diputar dan hukum kekekalan momentum sudut.

Baca sebelumnya : Momentum Sudut Benda (Partikel Bermassa) ǀ Pengertian, Penurunan Persamaan, & Contoh pada Kehidupan

MOMENTUM SUDUT BENDA KAKU YANG BERPUTAR

Perhatikan gambar benda kaku yang diputar pada gambar 1.1., sebuah lempengan dengan poros putar berada di pusat massa dan berputar terhadap sumbu z. Kita ambil sampel massa dari lempengan bernama mi, dimana mi diberi kecepatan linier (tangensial) vi dan memiliki jarak ri terhadap poros putar (rotational axis).

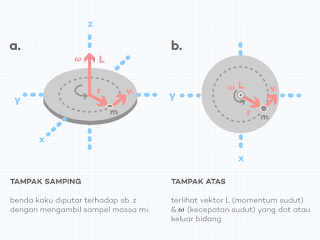Gambar 1.1. Sebuah Benda Kaku Diputar terhadap sb. z, Berikut Tampak Samping & Tampak Depannya

- klik gambar untuk melihat lebih baik -

Perhatikan arah vektor posisi ri, kecepatan linier vi, momentum sudut L, momentum linier p, dan kecepatan sudut ω, vektor L menuju atas, begitupula vektor ω. Cara menentukan arah vektor L dan ω adalah dengan kaidah tangan kanan. Sedangkan, kemana arah vektor p (momentum linier)? Arah vektor momentum linier adalah searah dengan kecepatan linier vi.

Baca juga : Vektor ǀ Cara Penjumlahan dan Pengurangan Vektor Beserta Contohnya untuk melihat cara menentukan arah vektor dengan kaidah tangan kanan.

Ingat! Simbol yang tebal pada gambar menandakan ia adalah besaran vektor.

Sebagaimana momentum linier, momentum sudut berarti terjadi pada massa yang bergerak memutar. Kita dapat menurunkan persamaan momentum sudut (L) benda kaku dari persamaan momentum sudut sebelumnya, yaitu L=m x p. Perhatikan penurunan persamaan pada gambar 1.2.

Gambar 1.2. Penurunan Persamaan Momentum Sudut Benda Kaku yang Diputar, Hubungannya dengan Momen Inersia, & Hukum Kekekalan Momentum
- klik gambar untuk melihat lebih baik -

1. Momentum sudut dari benda kaku dengan sampel massa bernama mi. Tidak masalah, karena kita akan menjumlahkan seluruh sampel massa nantinya dan kita mendapati persamaan momentum sudut total.

Subtitusi persamaan momentum linier, lalu persamaan kecepatan linier ke persamaan pertama

2. Menjumlahkan momentum sudut total dari seluruh sampel massa benda kaku dengan menggunakan fungsi sigma. Kini, kita memiliki persamaan sudut pada benda kaku yang diputar.

3. Kita coba turunkan persamaan momentum sudut dan diperolehlah persamaan momen gaya (torsi) benda kaku tersebut. Ternyata, turunan dari momentum sudut adalah momen gaya (torsi), L = Iω

HUKUM KEKEKALAN MOMENTUM

Pada persamaan terakhir penurunan persamaan gambar 1.2. adalah gambaran sebuah keadaan saat benda yang berputar berubah bentuk. Hukum kekekalan momentum ini berlaku untuk kondisi dimana benda berputar pada ruang bebas gesekan (lantai atau udara) atau sistem terisolasi.

Contoh hukum kekekalan momentum pada kehipan nyata saah satunya adalah seorang atlet icekating meluncur kemudian berputar dengan tangan mendekap di depan dada.

Kecepatan berputarnya (ω) sangat besar begitupula momentum sudutnya (L). Jari-jari dari atlet sebagai benda kaku adalah kecil (r) karena ia mendekapkan kedua tangannya ke dada. Lalu, ia membentangkan tangannya. Misal, nilai ω=10, I=2 didapat dari jari-jari (r), dan L = I.ω=20.

Seketika, atlet membentangkan kedua tangannya. Kini, ia berputar lebih pelan. Kecepatan sudutnya (ω) berkurang. Hal ini karena atlet memperbesar momen inersianya dengan memperbesar jari-jarinya (r). Pada keadaan ini, momentum sudut atlet adalah kekal, sehingga saat momen inersianya diperbesar, kecepatan sudutnya mengecil (ω). Misal, nilai ω=5, I=4 didapat dari jari-jari (r), dan L = I.ω=20

Jadi, kita dapat menyimpulkan bahwa momentum sudut bendakaku yang dippuat adalah L= Iω, dan hukum kekekalan momentum sudut berlaku pada sistem terisolasi, energi total benda, momentum linier, dan momoentum sudutnya kekal.