Hukum Utama Hidrostatis ǀ Tekanan pada Pipa U, Persamaan (Rumus), dan Analisis Gambar

Kita telah membahas pengertian tekanan hidrostatis, penurunan persamaan tekanan hidrostatis. Sekarang, kita akan lanjut pada penerapan tekanan hidrostatis pada pipa U dengan luas kolom kanan-kiri sama besar. Penerapan ini merupakan aplikasi hukum utama hidrostatis.

Hukum utama hidrostatis menyatakan bahwa titik yang sejajar horisontal pada fluida yang diam (statis) memiliki tekanan yang sama besar.

Perhatikan gambar 1.1.a., 1.1.b., 1.1.c., dan 1.1.d!

Titik A dan B adalah sejajar secara horisontal dan berada pada jarak kedalaman yang sama dari permukaan. Tekanan pada kedua titik ini adalah sama besar, dimana fluida berada dalam kondisi statis.

Ingat! Tekanan adalah besaran skalar. Gaya-lah yang memiliki arah karena vektor.

Baca sebelumnya : Tekanan Hidrostatis ǀ Pengertian, Persamaan (Rumus), Manometer & Barometer, Tekanan Mutlak & Gauge (Hidrostatis)

ANALISIS GAMBAR & PENURUNAN PERSAMAAN FLUIDA PADA PIPA U

Gambar 1.1. Soal Hukum Utama Hidrostatis pada Fluida yang Berbeda-beda dalam Pipa U yang Dicari Tekanannya

Massa jenis 1 (biru) > Massa jenis 2 (kuning)> Massa jenis 3 (merah)

- klik gambar untuk melihat lebih baik -

Gambar 1.2. Cara Analisa Tekanan pada Titik A dan B Pipa U dengan Variasi Fluida
Panah menunjukkan gaya yang bekerja pada titik A dan B

- klik gambar untuk melihat lebih baik -

GAMBAR 1.1.A.

Fluida satu dimasukkan dalam pipa U. Tinggi kolom fluida satu kanan dan kiri adalah sama. Hal ini terjadi karena tekanan di titik kanan dan kiri yang sejajar selalu sama besar. Tidak hanya pada titik A dan B.

Fluida berada dalam keadaan statis, berarti resultan gaya pada pipa U adalah nol.

GAMBAR 1.1.B.

Fluida berada dalam keadaan statis (diam, tenang, tidak bergerak), berarti ia dalam posisi setimbang, resultan gayanya dalah nol. Kita masukkan fluida dua pada kolom sebelah kiri. Ia menekan fluida satu hingga terdorong sejauh h1.

Kita ambil titik yang memiliki tekanan sama besar, yaitu titik A dan B. Salah satu titik harus berada pada perbatasan antara dua jenis fluida ini, yaitu titik A. Gaya bekerja pada titik A oleh fluida dua (setinggi h2) dan gaya bekerja pada titik B oleh fluida satu (setinggi h1) atau fluidanya sendiri.

Pada kondisi ini, massa jenis fluida satu lebih besar dari fluida dua. Persamaan gambar 1.1.b., dapat dilihat pada gambar 1.3.

GAMBAR 1.1.C.

Kita variasi dengan memasukkan fluida dua dan tiga bersamaan di kolom kiri pipa U. Tampak massa jenis fluida dua lebih besar dari fluida tiga. Itu sebabnya dia berada di bawah fluida tiga.

Sedangkan, massa jenis fluida satu lebih besar dari fluida dua. Massa jenis fluida satu tidak mungkin lebih kecil dari fluida dua atau tiga. Hal ini akan menjaga posisi fluida satu tetap di bawah. Layaknya minyak dan air, es dan air, massa jenis paling kecil akan selalu di atas.

Analisis gaya yang bekerja pada titik A dan B dapat dibayangkan seperti petunjuk gambar 1.2.

GAMBAR 1.1.D.

Sekarang, kita letakkan fluida dua di kolom kanan dan fluida tiga di kolom kiri. Jika tanpa fluida tiga, maka h1 akan lebih tinggi lagi. Kita tahu bahwa massa jenis fluida satu > massa jenis fluida dua > massa jeinis fluida tiga. Penurunan persamaan pada kondisi ini dapat dilihat pada persamaan 1.3.

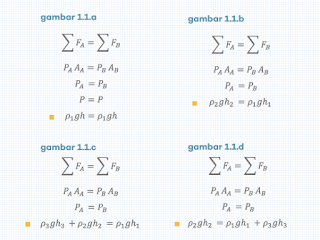Gambar 1.3. Persamaan Tekanan atau Resultan Gaya pada Penerapan Hukum Utama Hidrostatis (Pipa U) dengan Variasi Jenis Fluida

- klik gambar untuk melihat lebih baik -

Baca selanjutnya: Hukum Pascal ǀ Bunyi, Persamaan (Rumus), & Dongkrak Hidrolik

Kesimpulannya adalah tekanan pada titik yang sejajar secara horisontal memiliki besar yang sama selama fluida tersebut statis.