Bilangan Euler, Metode Euler, Log, & Ln ǀ Pengertian, Hubungan, Contoh Soal, & Penerapannya dalam Fisika

Pembahasan kali ini akan mengupas tuntas perbedaan antara bilangan euler dan metode euler serta hubungannya dengan log dan ln. Berikut pengertian, hubungan, contoh, dan penerapannya dalam kehidupan.

Mungkin akan muncul pertanyaan dalam benak kita tentang penerapan fisika yang begitu kompleks di lapangan. Bagaimana menghitung kecepatan atau percepatan sebuah benda yang mulanya melesat di udara kemudian ia jatuh ke dalam air? Percepatan & kecepatannya benda dalam dua medium ini tentu akan berbeda.

Hal ini akan semakin rumit saat seorang amatir harus menghitung dengan analisis yang cepat, cukup tepat, dan tidak terlalu sulit. Situasi ini diperlukan model numerik. Salah satu model numerik termudah adalah Metode Euler.

Muncul beberapa pertanyaan lagi tentang metode Euler. Apakah metode Euler? Hubungan Euler dengan logaritma natural/ alami (ln) atau log? Hubungan Euler dengan turunan atau integral? Mengapa Euler ini lebih mudah dari pada analisis turunan atau integral? Bagaimana contoh kasus nyata dengan penerapan Euler? Kita akan membahasnya.

FUNGSI EKSPONEN ALAMI (EULER)

Bahasan akan dimulai dari apa itu e atau lambang dari konstanta Euler karena penambahan kata “metode” dalam Metode Euler memberikan maksud yang berbeda. Metode Euler hanyalah cara sederhana untuk mendekati nilai dari perhitungan eksak si fungsi eksponen alami. Ia bukan Euler itu sendiri. Setelah membaca tuntas, kita tidak akan pusing.

Euler (dibaca: oiler) dikenal dengan simbol e dari nama Leonhard Euler (1701-1783). Ia begitu spesial layaknya π sehingga ia perlu memiliki simbol tersendiri. Bilangan atau konstanta e muncul sebagai basis (bilangan yang dipakai rujukan) dari fungsi eksponen atau logaritma. e merupakan bilangan real positif yang unik. e ≈ 2,718 281 828 459 045.

Logaritma mempunya beberapa bilangan basis yang sering digunakan. Basis logaritma yang sering digunakan adalah logaritma biasa basis 10 (log) dan logaritma alami (ln). Fungsi logaritma alami dan fungsi logaritma basis e adalah invers dari fungsi eksponen alami (exp), dimana exp identik dengan e.

Gambar 1.1. Jenis Fungsi, Hubungan Fungsi Logaritma Alami, Logaritma, & Eksponen
- klik gambar untuk melihat lebih baik -

Apakah kita perlu mendapat basis yang lain? Tidak. Kita dapat mengganti basis dengan eksponen lain. Kita tinggal memadankannya dengan formula yang sudah ada.

Berikut hubungan antara konstanta euler, log, dan ln.

Gambar 1.2. Fungsi Eksponen Alami (exp). Hubungan antara ln, log, exp, & e
- klik gambar untuk melihat lebih baik -

METODE EULER

Pada gerak benda, selisih waktu Δt bisa jadi sangat kecil seperti mikrosekon. Metode Euler muncul sebagai suatu cara dalam menyelesaikan persamaan turunan dengan rasio selisih terbatas. Ia dapat melakukan pendekatan hasil yang sama dengan perhitungan eksak dari persamaan turunan.

Keakuratan dari metode Euler akan sangat bergantung pada ukuran kenaikan yang digunakan. Semakin kecil akan semakin mendekati benar. Kita sepertinya memang perlu tahu hasil perhitungan secara eksak sebagai pembanding hasil. Kita akan semakin paham bedanya saat membaca contoh soal.

Gambar 1.3. Metode Euler (Pendekatan Hasil Perhitungan Eksak yang Melibatkan Bilangan Euler) pada Penerapan Fisika Gerak Dipercepat
- klik gambar untuk melihat lebih baik -

PENERAPAN DALAM FISIKA

Bilangan Euler digunakan dalam penyelesaian proses hitung pada beberapa kasus fisika. Contohnya adalah proses peluruhan, pertumbuhan, dan gerak partikel. Kita akan membahas tentang gerak partikel. Fungsi ini dapat digunakan dalam menghitung kenaikan waktu yang kecil dengan ukuran kenaikan terbatas.

CONTOH SOAL PERHITUNGAN EKSAK DAN METODE

Benda bermassa 2,00 gr jatuh dalam wadah besar berisi minyak. Benda tersebut bergerak dalam minyak dan mendapat gaya berlawanan yang sebanding dengan kecepatannya. Benda tersebut mencapai kelajuan terminal 5,00 cm/s. Tentukan konstanta waktu т dan kapan benda mencapai 90,0 % dari kelajuan terminalnya

Baca : Gerak yang Dipengaruhi Gaya Hambat agar tahu asal mula persamaan di atas.

Gambar 1.4. Cara Perhitungan Eksak yang Melibatkan Bilangan Euler untuk mencari selang waktu benda untuk mencapai 90,0% kelajuan terminalnya
- klik gambar untuk melihat lebih baik -

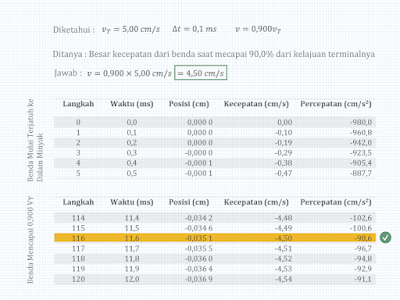Gambar 1.5. Cara Perhitungan dengan Pendekatan Hasil agar sesuai dengan Perhitungan Eksak Sebelumnya (Metode Euler)
- klik gambar untuk melihat lebih baik -

Pada cara satu atau penggunaan fungsi eksponen alami yang melibatkan bilangan Euler atau exp, kita mendapatkan hasil yaitu 11,7 ms. Saat kita menggunakan metode Euler kita mendapatkan jawaban yang berbeda yaitu, 11,6 ms. Tentu jawaban ini bisa menjadi 11,7 seperti hitungan eksak dengan syarat selisih waktunya diperkecil lagi.