5 Soal & Pembahasan Katrol-Tali Dinamika Partikel pada Lantai ǀ Penurunan Persamaan & Analisisnya

Dinamika partikel pada pesawat atwood (katrol-tali) memiliki variasi yang cukup banyak. Mulai dari variasi bidang, gaya gesek, massa tali dan katrol diabaikan atau tidak diabaikan. Nah, kita akan menurunkan persamaan dinamika partikel dengan tali dan katrol yang diabaikan. Berikut analisisnya.

Beberapa variasi benda bermassa diikat pada ujung tali yang dihubungkan dengan katrol. Benda diletakkan pada lantai yang licin ataupun kasar. Akibat gaya berat, benda bergerak dengan percepatan (a) dan gaya tegang tali (T) muncul.

Katrol dianggap tak bermassa dan bebas gesekan. Begitupula dengan tali yang digunakan, ia tidak dapat meregang dan tak bermassa. Kita hanya akan menganalisis gaya yang berkerja pada alat ini. Berikut variasi contohnya.

PESAWAT ATWOOD 1

Sebuah beban bermassa m₁ dan m₂ dikaitkan pada tali seperti pada gambar. Lantai permukaan benda m₁ memiliki gaya gesek kinetik sebesar f_k. Massa m₂ lebih besar daripada m₁ sehingga semua benda bermassa dan tali bergerak searah jarum jam.

Gambar 1.1. Dinamika Gerak Katrol (Pesawat Atwood) Contoh Satu
-klik gambar untuk melihat lebih baik-

Percepatan a akan searah jarum jam, percepatan g tetap akan ke bawah, gaya tegang tali pada semua bagian tali adalah sama besar. Benda m₁ memiliki gaya pada komponen x dan y, sedangkan benda m₂ hanya memiliki gaya pada komponen y.

Gambar 1.2. Penurunan Persamaan Gaya pada Dinamika Gerak Katrol (Pesawat Atwood) Contoh Satu
-klik gambar untuk melihat lebih baik-

Besar gaya tegang tali (T) akan sama besar walau berbeda arah. Kita hanya perlu menambahkan tanda positif, jika T searah dengan a dan negatif, jika T berlawanan arah dengan a. Jika kita ingin memperoleh persamaan gaya tegang tali yang lain, maka kita dapat mensubtitusikan persamaan a pada persamaan T sembarang.

PESAWAT ATWOOD 2

Lantai permukaan benda m₁ licin tanpa gaya gesek. Massa m₂ lebih besar daripada m₁ sehingga semua benda bermassa dan tali bergerak searah jarum jam. Benda m₁ memiliki gaya pada komponen x dan y, sedangkan benda m₂ hanya memiliki gaya pada komponen y.

Gambar 2.1. Dinamika Gerak Katrol (Pesawat Atwood) Contoh Dua
-klik gambar untuk melihat lebih baik-

Gambar 2.2. Penurunan Persamaan Gaya pada Dinamika Gerak Katrol (Pesawat Atwood) Contoh Dua
-klik gambar untuk melihat lebih baik-

Perhatikan perbedaan sumbu x dan y pada masing-masing beban. Sumbu x pada m₁ akan mengikuti bidangnya yang miring, sedangkan sumbu x pada m₂ akan horisontal biasa. Walau sumbu x atau y pada keduanya berbeda, tetapi kita sudah mengatasinya dengan melibatkan fungsi sin dan cos. Kita tidak perlu mempermasalahkannya.

PESAWAT ATWOOD 3

Lantai permukaan benda m₂ licin tanpa gaya gesek. Massa beban m₃>m₂>m₁, sehingga semua benda bermassa dan tali bergerak searah jarum jam. Benda m₁ dan m₃ memiliki gaya pada komponen y, sedangkan benda m₂ memiliki gaya pada komponen x.

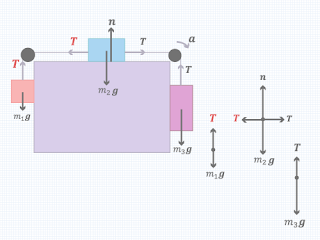Gambar 3.1. Dinamika Gerak Katrol (Pesawat Atwood) Contoh Tiga
-klik gambar untuk melihat lebih baik-

Gambar 3.2. Penurunan Persamaan Gaya pada Dinamika Gerak Katrol (Pesawat Atwood) Contoh Tiga
-klik gambar untuk melihat lebih baik-

Gaya yang menyebabkan pesawat atwood ini bergerak hanyalah gaya pada komponen y yang dimiliki oleh m₁ dan m₃. Beban m₂ hanya mengakibatkan percepatan melambat pada sistem. 

Ingat! gaya adalah penyebab percepatan.

Gaya tegang tali (T) dan gaya tegang tali (T) memiliki nilai yang berbeda. Hal ini terjadi karena keduanya berada pada tali yang berbeda. Nilai T (gaya tegang tali antara m₁ dan m₂) ≠ T (gaya tegang tali antara m₂ dan m₃).

PESAWAT ATWOOD 4

Lantai permukaan benda m₁ dan m₂ adalah bidang miring dengan sudut berbeda yang licin tanpa gaya gesek. Massa beban m₂>m₁, sehingga semua benda bermassa dan tali bergerak searah jarum jam. Benda m₁ dan m₂ memiliki gaya pada komponen x dan y.

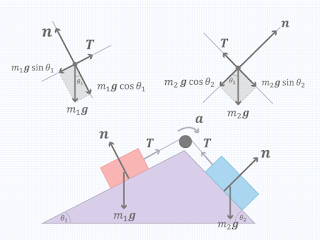Gambar 4.1. Dinamika Gerak Katrol (Pesawat Atwood) Contoh Empat
-klik gambar untuk melihat lebih baik-

Gambar 4.2. Penurunan Persamaan Gaya pada Dinamika Gerak Katrol (Pesawat Atwood) Contoh Empat
-klik gambar untuk melihat lebih baik-

Penggambaran sumbu x dan y kedua beban memiliki perbedaan, dimana sumbu x selalu sejajar dengan bidang benda tersebut dan y tegak lurus terhadapnya. Kasus ini sama hal dengan pesawat atwood 2, dimana permasalahan ini sudah ditanngani dengan sin dan cos. Kini, kita dapat menganggap keduanya sama saja.

PESAWAT ATWOOD 5

Sebuah beban bermassa m₁, m₂, dan m₃ dikaitkan pada tali seperti pada gambar. Lantai permukaan benda m₁ adalah datar bebas gaya gesek. Massa m₁ lebih kecil daripada m₂+m₃ sehingga semua benda bermassa dan tali bergerak searah jarum jam.

Gambar 5.1. Dinamika Gerak Katrol (Pesawat Atwood) Contoh Empat 
-klik gambar untuk melihat lebih baik-

Gambar 5.2. Penurunan Persamaan Gaya pada Dinamika Gerak Katrol (Pesawat Atwood) Contoh Lima
-klik gambar untuk melihat lebih baik-

Percepatan a akan searah jarum jam, percepatan g tetap akan ke bawah, gaya tegang tali pada semua bagian tali yang mengubungkan m₁ dan m₂ adalah sama besar kecuali gaya tegang tali antara m₂ dan m₃. Benda m₁ memiliki gaya pada komponen x dan y, sedangkan benda m₂ dan m₃ hanya memiliki gaya pada komponen y.

Ingat! Bagaimana mungkin tali yang digantungi m₂ dan m₃ akan memiliki gaya tegang yang sama besar denga tali yang hanya digantungi oleh m₃?. Sehingga untuk mencari gaya tegang tali antara m₁ dan m₂, kita akan menganggap m₂ dan m₃ adalah satu kesatuan massa. Kemudian, kita akan menganalisis gaya tegang tali antara m₂ dan m₃.

Nilai T (gaya tegang tali antara m₂ dan m₃) ≠ T (gaya tegang tali antara m₁ dan m₂).

Baca juga : 

• Cara Menurunkan Persamaan Gaya Tegang Tali & Percepatan Katrol ǀ Pesawat Atwood
• Gaya Tegang Tali pada Benda Digantung ǀ Pengertian, Analisis Persamaan, & Diagram Gaya
• Gaya Normal ǀ Pengertian, Penurunan Persamaan, Contoh, & Efek Mangkok Penghisap

Itulah soal dan pembahasan katrol & tali pada benda bermassa alias pesawat atwood. Penurunan persamaan dan cara analisis persamaan secara garis besar dapat dilihat pada pembahasan sebelumnya.

Share this post