Perkalian Vektor ǀ Dot Product dan Cross Product, Pengertian & Contohnya

Apakah itu dot product (perkalian dot) dan cross product (perkalian silang)? Berikut penjelasan terkait dua jenis perkalian vektor ini sekaligus pengertian dan contohnya.

Vektor bisa dikali? Tentu. Saya harap anda sudah tau apa itu "besaran vektor dan besaran skalar pada fisika". Besaran vektor adalah besaran yang memiliki nilai dan arah, seperti kecepatan, gaya, dsb. Sedangkan, besaran skalar adalah besaran yang memiliki nilai saja, seperti suhu, energi.

Nah, kita akan bahas perkalian antara vektor dan vektor. Hasil dari perkalian ini bisa vektor, bisa skalar.

Cross Product
Vektor x Vektor = Vektor

Dot Product
Vektor x Vektor = Skalar

Lalu, bagaimana dengan perkalian fisika yang lain? Misal, vektor dikali skalar atau perkalian lainnya. Kita akan menyebutnya perkalian langsung (direct product) yang hasilnya berupa tensor atau matriks.

Kegunaan perkalian vektor dalam fisika adalah mengetahui nilai dari hasil perkalian vektor tersebut atau mengetahui nilai dengan arah dari hasil perkalian vektor tersebut atau melakukan penurunan persamaan. Berikut salah satu contoh penerapan perkalian vektor untuk cross product.

Gambar 1.1. Contoh Penerapan Cross Product dalam Perhitungan Fisika
Mengalikan besaran vektor (perpindahan) dan besaran vektor (kecepatan sudut) yang hasilnya berupa besaran vektor (kecepatan linier)
- klik gambar untuk melihat lebih baik -

1. PERKALIAN TITIK (DOT PRODUCT)

Dot Product dapat disebut juga produk skalar (scalar product) atau perkalian titik. Perkalian ini disebut perkalian titik karena kita memberi titik gemuk (fat dot) diantara perkalian vektor.

Perkalian titik adalah perkalian antar vektor yang menghasilkan besaran skalar (nilai tanpa arah). Perkalian ini memiliki aturan tertentu yang jelas berbeda dengan perkalian silang (cross product). Berikut aturan dari perkalian titik dapat dilihat pada gambar 1.2.

Misal, vektor a = (a_xi + a_yj + a_zk) dan vektor b = (b_xi + b_yj + b_zk). Saat kedua vektor dikalikan, kita dapat menggunakan cara sebagaimana contoh soal pada gambar 1.2.

Gambar 1.2. Dot Product yang Menghasilkan Besaran Skalar beserta Contohnya
- klik gambar untuk melihat lebih baik -

Contoh perkalian titik ini adalah W (Usaha) = F (Gaya) . s (Perpindahan), gaya dan perpindahan adalah besaran vektor dan hasil perkalian mereka adalah usaha yang notabene-nya energi yang merupakan besaran skalar.

2. PERKALIAN SILANG (CROSS PRODUCT)

Cross Product disebut juga produk vektor (vector product)/ perkalian silang. Perkalian ini disebut perkalian silang karena kita memberi silang diantara vektor (cross).

Perkalian silang adalah perkalian antar vektor yang menghasilkan besaran vektor (nilai dan arah). Perkalian ini memiliki aturan yang berbeda dengan perkalian titik (dot product). Berikut aturan dari perkalian silang dapat dilihat pada gambar 1.3 di bawah ini.

Gambar 1.3. Cross Product yang Menghasilkan Besaran Vektor beserta Contohnya
- klik gambar untuk melihat lebih baik -

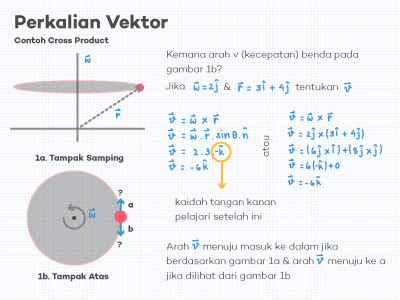
Gambar 1.4. Cara Menghitung a cross b dan Cara Menentukan Arah Vektor dengan Kaidah Tangan Kanan
- klik gambar untuk melihat lebih baik -

Contoh perkalian silang adalah τ (Momen gaya) = F (Gaya) x r (Perpindahan), perindahan dan gaya adalah besaran vektor, sedangkan hasilnya adalah momen gaya (torsi) yang merupakan besaran vektor juga.

CATATAN

Pada beberapa buku, vektor dituliskan dengan huruf bertanda panah di atas/ huruf tebal/ huruf bertanda mutlak. Beberapa buku juga, vektor satuan tidak hanya dituliskan dengan i topi, j topi, dan k topi melainkan dengan x topi, y topi, dan z topi.

KESIMPULAN

Perkalian vektor adalah perkalian antara vektor dan vektor. Jika hasilnya skalar, maka disebut dot produt (perkalian titik). Jika hasilnya vektor, maka disebut cross product (perkalian silang). Pengertian dan contoh telah dipaparkan sebagaimana di atas.